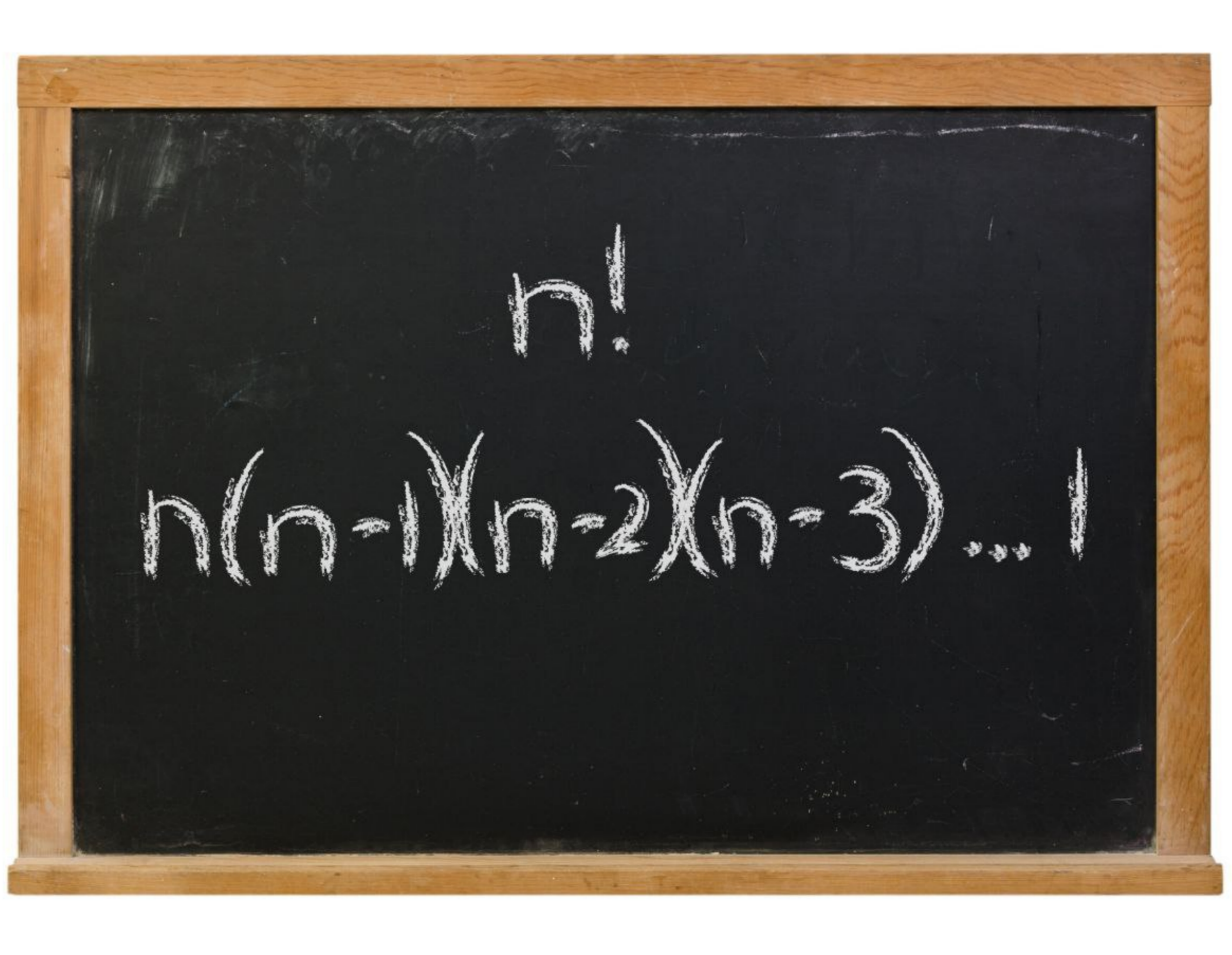
30 kişilik sınıftan bir başkan bir başkan yardımcısı seçilecektir. Kaç farklı şekilde seçilebilir? Olasılık hesapları yaparken kaçınılmaz olarak permütasyon ve kombinasyon hesapları yapılır. Unuttuysanız şöyle hatırlatayım, sıralama önemliyse permutasyon değilse kombinasyon kullanılıyordu. Permütasyonun matematiksel ifadesi şu şekilde:

P(n,r)=\frac {n!}{(n-r)!}

Bu işlemi gerçekleştirebilmek için faktöriyel hesabını önce kodlamamız gerekecek. Daha önce bir çok örnek yaptık. Şurada o kodları bulabilirsiniz.

1. Faktöriyel
2. Fonksiyonel programlama
3. Bir ben var bende

Burada tekrar faktöriyel hesabı anlatılmayacak onun yerine sanki o kod faktoriyel() şeklinde fonksiyon yazılmış olarak kabul edilerek ikinci bir fonksiyon olarak kod yazılacak.

def permutasyon(n, r):
    return faktoriyel(n) / faktoriyel(n-r)

Çok basit değil mi? Fonksiyonun girdilerini (input) tanımladık önce n ve r. sonrasında fonksiyonun çıktısını (output) tanımladık. Yukarıdaki matematiksel ifadeyi aslında aynen yazdık. faktoriyel() fonksiyonuna n‘in faktoriyelini hesaplatıp, ardından (n-1)‘in faktoriyelini hesaplattık. ve bunları bölerek çıktı olarak geri gönderdik. Yukarıdaki kodu kopyalayıp yapıştırmanıza rağmen siz sürekli hata alıyorsanız faktoriyel() fonksiyonunu tanımlamadınız demektir. Lütfen yukarıda 3 madde ile gösterilen linklerdeki kodlardan herhangi biriyle faktoriyel() fonksiyonunu oluşturun kod sayfanızda hemen altına da ikinci bir fonksiyon olarak şimdi yukarıda yazdığımız fonksiyonu yapıştırın. Sonra da en alt satıra print(permutasyon(30, 2)) yazın. Konsolda kodun çalıştığını göreceksiniz.

Sıra Sizde: 5 kişinin başvurduğu bir işe sadece 2 kişi alınacaktır. Bu 2 kişi kaç farklı şekilde seçilebilir? İşte buraya kombinasyonun matematiksel ifadesini yazıyorum. Lütfen bunun kodunu da siz yazar mısınız?

C(n,r)=\frac {n!}{(n-r)!\cdot  r!}