Mukavemet dersinde işlenmekte olan elastik eğrinin denkleminin çeşitli sınır şartlarında analitik olarak çözümünü Python sympy kütüphanesi kullanarak yapacağız.

from sympy import *
from sympy.abc import *

sympy kütüphanesindeki tüm fonksiyonları ve kullanabileceğimiz tüm sembol isimlerini çağırdık. Örneğin bir f(x,y,z) fonksiyonunun x, y ve z’ye bağlı olduğunu belirtmek için öncelikle x,y ve z’nin birer sembol olduğunu belirtmemiz gerekir. Bunu from sympy.abc import x,y,z şeklinde de yapabilirdik. Ancak ikinci satırda yazıldığı gibi tanımlanabilecek tüm sembolleri çağırmayı tercih ettik. Şimdi bir ince kirişin elastik eğri denklemini tanımlayalım. Aşağıda yayılı yük altındaki bir kirişin elastik eğri denklemi verilmiştir.

E I \frac{d^{4}}{d x^{4}} w{\left(x \right)} =- q

Python içerisinde yukarıdaki denklemi tanımlarken eşitliğin sağında bir verinin kalmaması gerekmektedir. -q değerini de denklemin soluna atarak Python içerisinde yazıyoruz.

w = Function("w")(x)
sol = E * I * w.diff(x, 4) + q

Kirişin çökme fonksiyonu w(x)’i analitik olarak elde edebilmek için yukarıdaki denklemi dört sefer integral almak gerekmektedir. Her bir integral sonunda bir adet bilinmeyen C katsayısı ortaya çıkmaktadır. Yani dört sefer integral aldıktan sonra elimizde dört adet bilineyen olacaktır.

C_{1} + E I \frac{d^{3}}{d x^{3}} w{\left(x \right)} + q x=0 \\
C_{1} x + C_{2} + E I \frac{d^{2}}{d x^{2}} w{\left(x \right)} + \frac{q x^{2}}{2}=0\\
\frac{C_{1} x^{2}}{2} + C_{2} x + C_{3} + E I \frac{d}{d x} w{\left(x \right)} + \frac{q x^{3}}{6} =0\\
\frac{C_{1} x^{3}}{6} + \frac{C_{2} x^{2}}{2} + C_{3} x + C_{4} + E I w{\left(x \right)} + \frac{q x^{4}}{24}=0

Yukarıda görülen bilinmeyen katsayıları (C₁ , C₂ , C₃ , C₄ ) elde edebilmek için dört adet sınır şartına ihtiyaç duyulmaktadır. Örneğin iki ucu basit mesnetli bir kiriş için sınır şartları:

w(0)=0, \quad w(L)=0, \quad \frac{d^{2}}{d x^{2}} w{\left(0 \right)}=0, \quad\frac{d^{2}}{d x^{2}} w{\left(L \right)}=0

Sınır şartlarını kullanarak bilinmeyen katsayılar elde edilir ve yer değiştirme denklemi w(x) elde edilir.

w(x)=\frac{q x \left(- L^{3} + 2 L x^{2} - x^{3}\right)}{24 E I}

Bu işlemleri Python içerisinde dsolve komutu ile kolayca yapabilirsiniz.

SS = dsolve(sol,
            ics={w.subs(x, 0): 0,
                 w.subs(x, L): 0,
                 w.diff(x,2).subs(x, 0): 0,
                 w.diff(x,2).subs(x, L): 0})
W = SS.rhs

Yukarıda W ile tanımladığımız denklem iki ucu basit mesnetli yayılı yük altındaki bir kirişin çökme denklemidir. Bulduğumuz denklemi kullanarak bir örnek çözelim.

q=0.1 \frac{N}{m} \\
L=100 \ mm \\
h=b=1 \ mm \\
E=210000 \ MPa

graphSS = plot(W.evalf(subs={L: 100,
                             E: 210000,
                             I: 1 / 12,
                             q: 0.1}), (x, 0, 100))

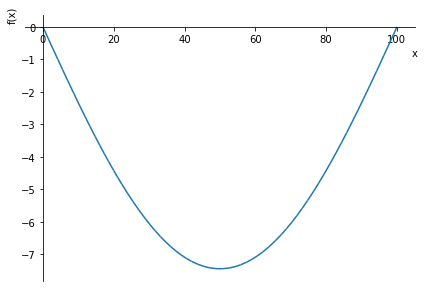
Aynı kirişin iki ucunun ankastre mesnetli olduğu durumu veya bir ucunun ankastre, diğer ucunun serbest olduğu durumları çözebilirsiniz.

Sıra sizde…