Yaygın kullanılan ve kolayca kodlanabilen bir yöntem olan trapez yöntemi şekilde de görüleceği üzere eğrinin altında kalan alanı yamuklara bölme ve bu yamukların alanlarını toplama işlemidir kabaca.

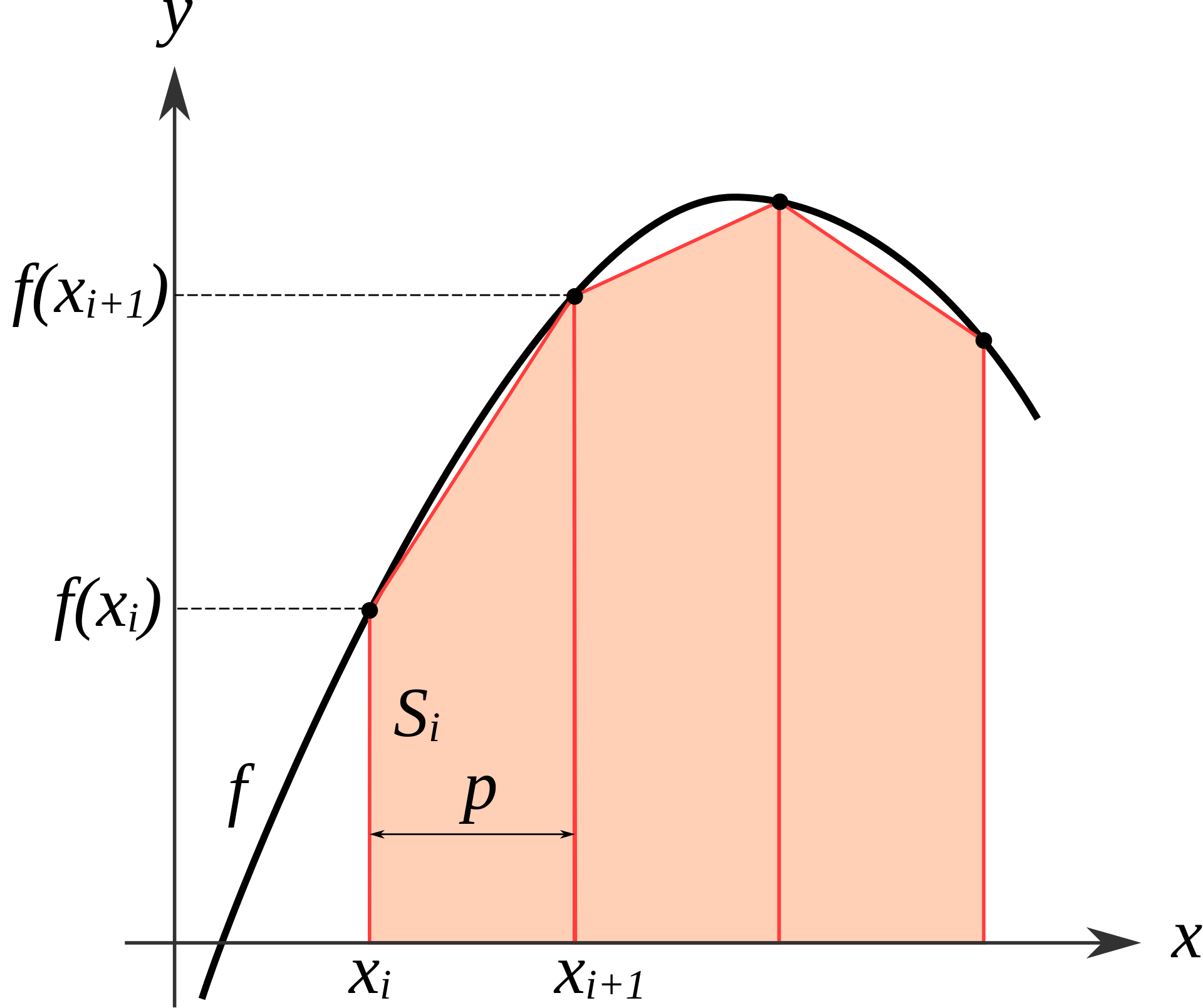
Yamuğun alanını hatırlarsak, paralel kenarların uzunluklarını toplayıp yarısını alıyorduk ve bunu aradaki mesafe ile çarpıyorduk. Denklem olarak ifade edersek, aşağıdaki form sanırım daha anlaşılabilir.

\int_{0}^{n} f(x) d x \approx \sum_{i=0}^{n} \frac{f\left(x_{i}\right)+f\left(x_{i+1}\right)}{2} \Delta x_{i} = \sum_{i=0}^{n} \frac{y_{i}+y_{i+1}}{2}(x_{i+1}-x_{i})

Şimdi de matematik dilinden Python diline çevirelim bu ifadeyi.

def trapez(y, x):
       alan = 0
       for i in range(len(x) - 1): 
          alan = alan + (y[i] + y[i + 1]) * (x[i + 1] - x[i]) / 2
       return alan

Fonksiyonun girdileri tabi ki eğriyi temsil eden x ve y kordinatlarını içeren listeler. Riemann da yaptığımız gibi denklemdeki toplam sembollü seriyi kodlamak için bir başlangıç değeri verdiğimiz değişken tanımlıyorduk ve her döngüde bu değişkenin içine hesapladığımız alanı atıyorduk. Benzer şekilde alan diye bir değişken oluşturuyoruz ve bunu 0 olarak belirliyoruz başlangıç değeri olarak.

Sonrasında döngü yazıyoruz ve döngünün dönme miktarı eğrinin altını böleceğimiz her bir yamuğun sayısı kadar olmalı. Bu da nokta sayısının bir eksiği olacaktır. Böylece range(len(x) – 1) ifadesiyle döngüyü x listesinin uzunluğunun bir eksiği kadar belirliyoruz.

Sonrasında döngünün içine yukarıdaki denklemi aynen yazıyoruz ve hep bir önceki alan değeriyle toplayarak, toplaya toplaya toplam alanı hesaplıyoruz. Yaptığımız işlemi şu şekilde görselleştirilebiliriz.

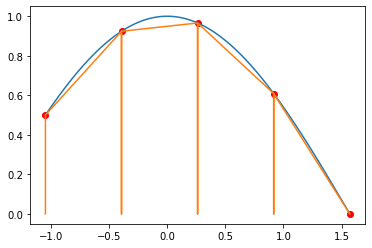
Aslında biz bu kadar anlatsak da bu işlemin numpy kütüphanesinde hazırı bulunuyor. np.trapz() ile yukarıdaki kodu yazmadan da kütüphane kullanarak işlemi hesaplayabiliriz. Aynı fonksiyona scipy.integrate.trapz() ile de ulaşılabilir.

Ders 2.3: Simposon Kuralıyla İntegral

Serdar Turgut İnce