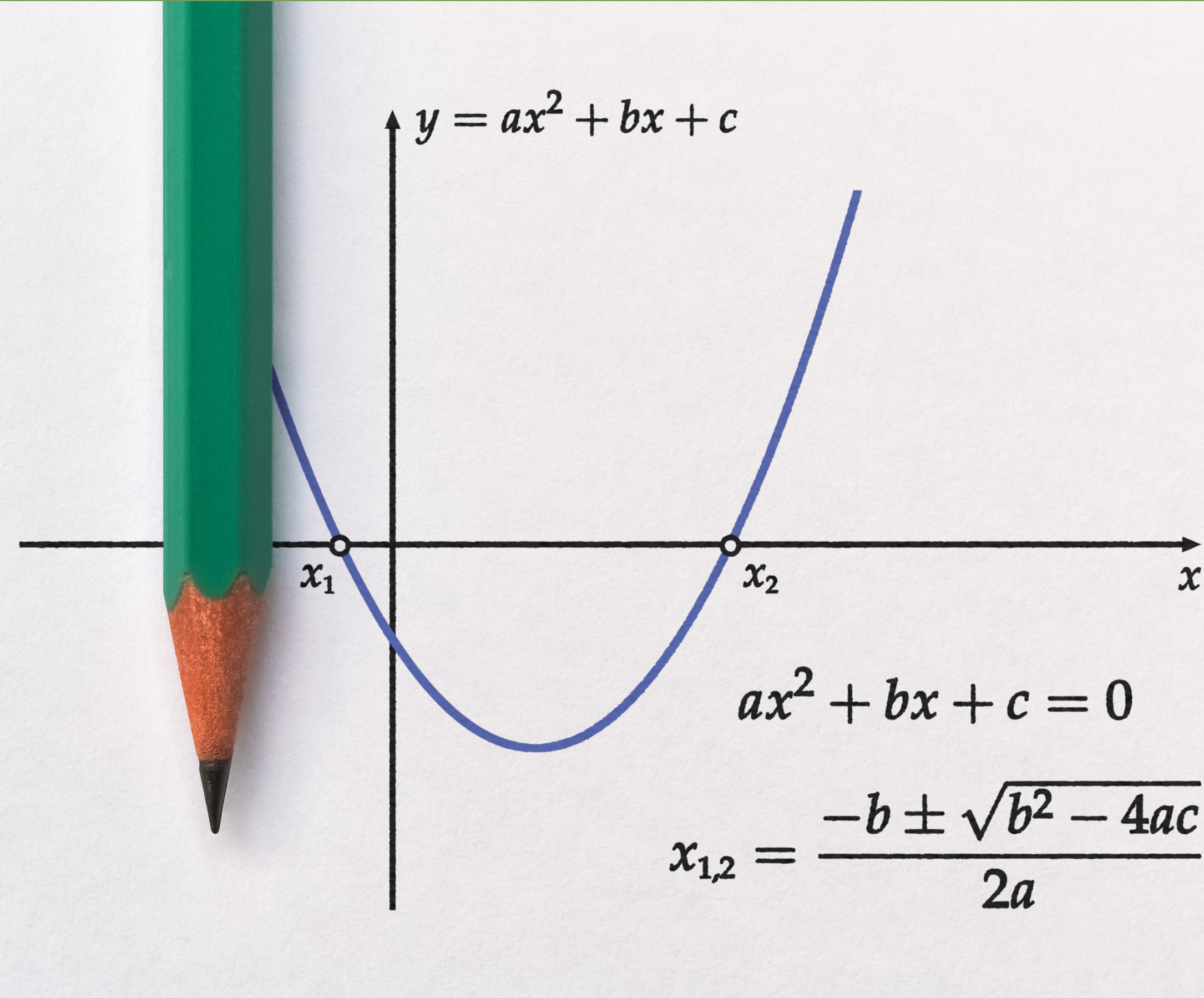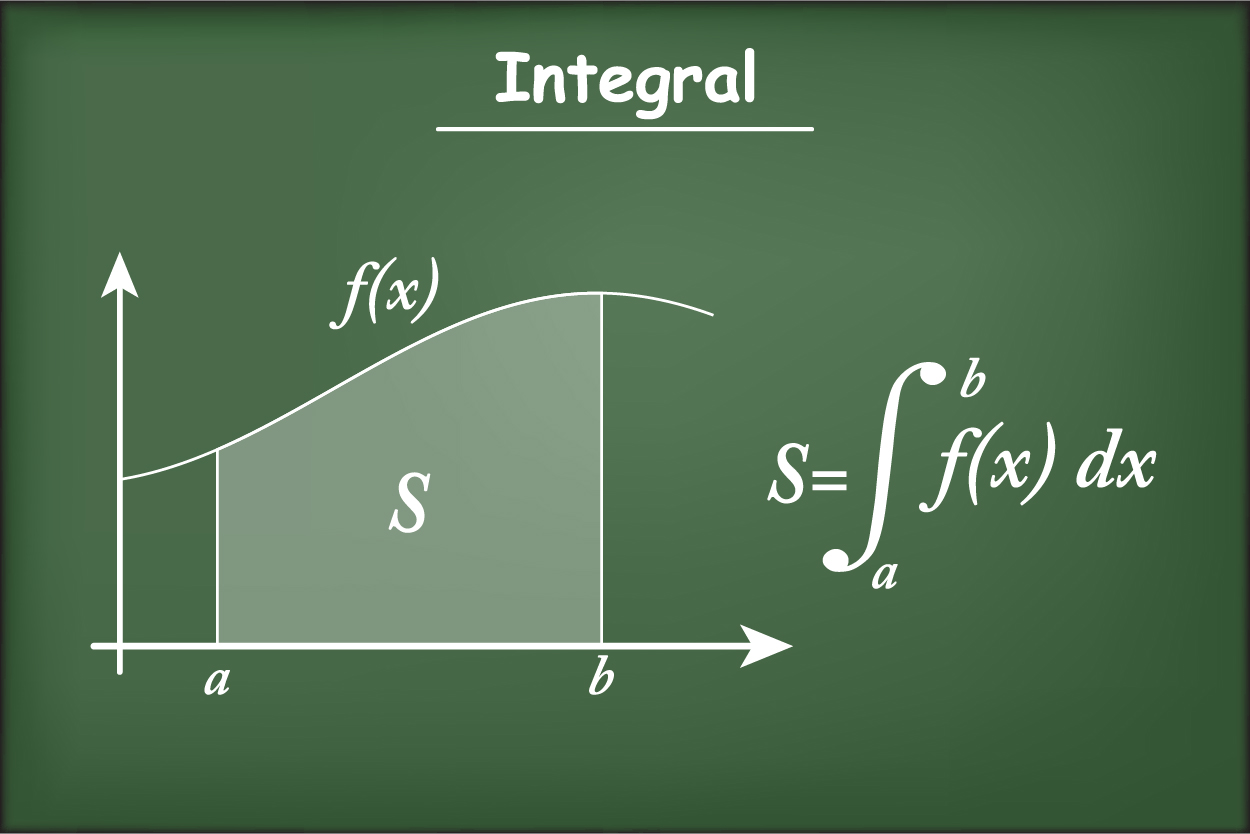
Simpson Kuralı
21 Şubat 2021
Yarılama Metodu
12 Nisan 2021
Şimdi de yazdığımız kodları kıyaslayalım. Bazı yöntemlerin farklı alt uygulamaları bulunsada, temelde 3 farklı yöntemle integral için kodlar yazdık, şimdi bildiğimiz bir fonksiyon için integral hesaplayalım. Bildiğiniz üzere cos(x)’in integrali sin(x) o zaman belirli bir integral yazalım.
\int_{-\pi/3}^{\pi/2} cos(x) d x=sin(\frac{\pi}{2}) -sin(-\frac{\pi}{3})\approx 1.866Şimdi pythonda bu fonksiyonu hesaplayıp kıyaslayalım
import numpy as np
x=np.linspace(-np.pi/3,np.pi/2,11)
y=np.cos(x)
gercek=np.sin(np.pi/2)-np.sin(-np.pi/3)
print("Gerçek değeri \t:",round(gercek,3))
riemann_left=riemann_left(y, x)
print("Riemann sol \t:",round(riemann_left,3))
riemann_cent=riemann_center(y, x)
print("Riemann merkez \t:",round(riemann_cent,3))
trapz=trapez(y, x)
print("Trapez \t\t\t:",round(trapz,3))
simp=simpson13(y, x)
print("Simpson1/3\t\t:",round(simp,3))
Sonuçlar şöyle:
Gerçek değeri : 1.866 Riemann sol : 1.921 Riemann merkez : 1.855 Trapez : 1.855 Simpson1/3 : 1.866
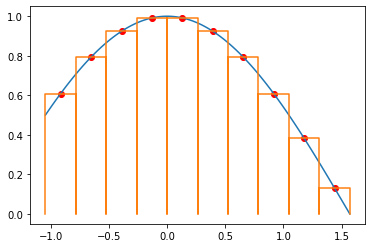
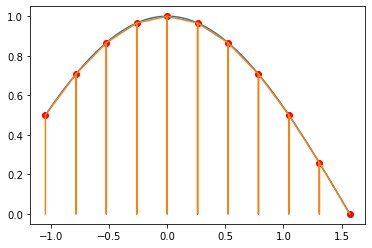
Görüleceği üzere en yakın sonucu tabi 3 haneye yuvarladığım için aynı görüyorsunuz, simpson yönteminde elde ettik. Hesaplamalarımızı görselleştirirsek şu şekilde oluyor.

Serdar Turgut İnce