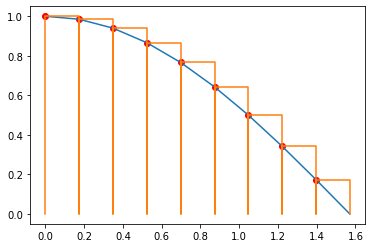
Bu kural eğrinin altında kalan alanları ufak dikdörtgenlere bölerek hesaplama yöntemi. Şekilde de görüleceği üzere bu işlem bir çok farklı şekilde yapılabilir. Dikdörtgenlerin yüksekliği dikdörtgenin sol üst köşesinin eğriye değen noktası alınabileceği gibi, sağında değdiği nokta ya da tam ortasının değdiği nokta alınabilir. Biz burada Riemann sol kuralını kullanacağız.

Riemann sol kuralı (yukarıdaki sarı grafik), bulunulan noktanın y değerini alıyor bir sonraki nokta ile x farkı alınarak çarpılıyor ve böylece o bölgedeki dikdörtgenin alanı hesaplanıyor. Bu işlem eğriyi temsil eden tüm noktalar için tekrarlanınca toplam eğri altında kalan hesaplanabiliyor. Sanırım işin matematiği durumu daha güzel ifade edebilir.

\int_{0}^{n} f(x) d x \cong \sum_{i=0}^{n} \Delta x_{i} \cdot f\left(x_{i}\right)=\sum_{i=0}^{n} y_{i}\cdot(x_{i+1}-x_{i})

Denklemdeki seriyi incelerseniz basitçe dikdörtgenin yüksekliği yi olarak alınmış, dikdörtgenin genişliği ise (xi+1-xi) alınmış toplam sembolü ile tüm bu ufak dikdörtgen alanları toplanmış. Hadi bu işlemi matematik dilinden Python programlama diline çevirelim.

def riemann_left(y, x):
       alan = 0
       for i in range(len(x) - 1): 
          alan = alan + y[i] * (x[i + 1] - x[i])
       return alan

Fonksiyonumuzun girdileri basitçe eğriyi temsil eden x ve y noktaları. Bu noktaları kullanarak altta kalan alanı hesaplayabiliriz. Yukarıdaki denklemin en sağındaki seriyi kodlayacağız. İşin içinde bir seri varsa bu kesinlikle for döngüsüdür. Peki eğrinin altını kaç küçük dikdörtgene böleceğiz. Bu döngünün dönüş sayısını belirlemek için önemli.

Şöyle düşünebiliriz, kaç nokta ile temsil ediyorsak eğriyi, bir eksiği kadar dikdörtgene bölünebilir eğrinin altı. Bunu da döngüdeki range(len(x)-1) ile ifade ettik. Böylece fonksiyona istediğimiz boyutta x ve y noktası gönderebiliriz. Parametrik olarak döngü sayısı da girdilerimizin boyutuna göre değişecektir.

Döngüden hemen önce alan=0 olarak başlangıç değeri oluşturduk. Sonrasında her döngüde yeni dikdörtgenin alanını hesaplayacağız ve önceki alanların üzerine ekleyeceğiz. Bu yöntem serilerin kodlanmasında bir kalıptır. Şöyle düşünebilirsiniz, markete gidip bir sepet aldınız her aldığınızı sepete atarak devam ediyorsunuz alışverişe. Serilerde de her işlem yaptığınızda bunu alan diye oluşturduğumuz sepete ekleyerek devam ediyoruz. Böylece son dikdörtgenin alanını da hesaplayıp alana eklersek, toplam eğri altında kalan alanı hesaplamış oluyoruz.

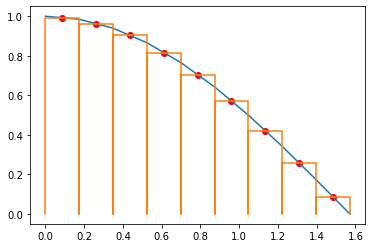
Madem balık tutmayı öğretmek amacımız, o zaman riemann merkez’i de siz kodlayın. Yukarıdakilere benzer şekilde olacak ancak denklemi şu şekilde:

\int_{0}^{n} f(x) d x \cong \sum_{i=0}^{n} \Delta x_{i} \cdot f\left(x_{i}\right)=\sum_{i=0}^{n} \frac {(y_{i}+y_{i+1})}{2}\cdot(x_{i+1}-x_{i})

Denklemi kafanızda görselleştirmek için şu grafik size yardımcı olabilir.

Ders 2.2: Trapez Yöntemiyle İntegral

Serdar Turgut İnce