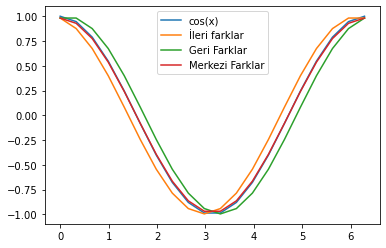
Örnek bir uygulama yaparsak bir sinüs eğrisinin ileri, geri ve merkezi farklarla türevini hesaplayalım, ve sinüsün türevi olan cosünüs eğrisiyle kıyaslayalım.
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 2 * np.pi, 20)
y = np.sin(x)
z = np.cos(x)
f = forward(y, x)
b = backward(y, x)
c = central(y, x)
plt.plot(x, z, x, f, x, b, x, c)
plt.legend(["cos(x)","İleri farklar", "Geri Farklar", "Merkezi Farklar"])
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 2 * np.pi, 20)
y = np.sin(x)
z = np.cos(x)
f = forward(y, x)
b = backward(y, x)
c = central(y, x)
plt.plot(x, z, x, f, x, b, x, c)
plt.legend(["cos(x)","İleri farklar", "Geri Farklar", "Merkezi Farklar"])
import matplotlib.pyplot as plt import numpy as np x = np.linspace(0, 2 * np.pi, 20) y = np.sin(x) z = np.cos(x) f = forward(y, x) b = backward(y, x) c = central(y, x) plt.plot(x, z, x, f, x, b, x, c) plt.legend(["cos(x)","İleri farklar", "Geri Farklar", "Merkezi Farklar"])
Yalnız yukarıdaki kodları biraz güncellemeniz gerekecek, Çünkü eksenlerin boyutlarını eşitleyebilmek için bir başlığın sonundaki paragrafta anlatılan şekilde ileri farkların son noktasına geri fark hesaplandı. Geri farkın ilk noktasına ileri fark hesaplandı. Merkezi fark için ilk ve son noktasına ileri ve geri fark hesaplanarak eksenlerin boyutları eşitlendi. Sonuç olarak şu grafik elde edildi.
Sorularınızı yorumlar kısmından yazmayı unutmayın.
Serdar Turgut İnce