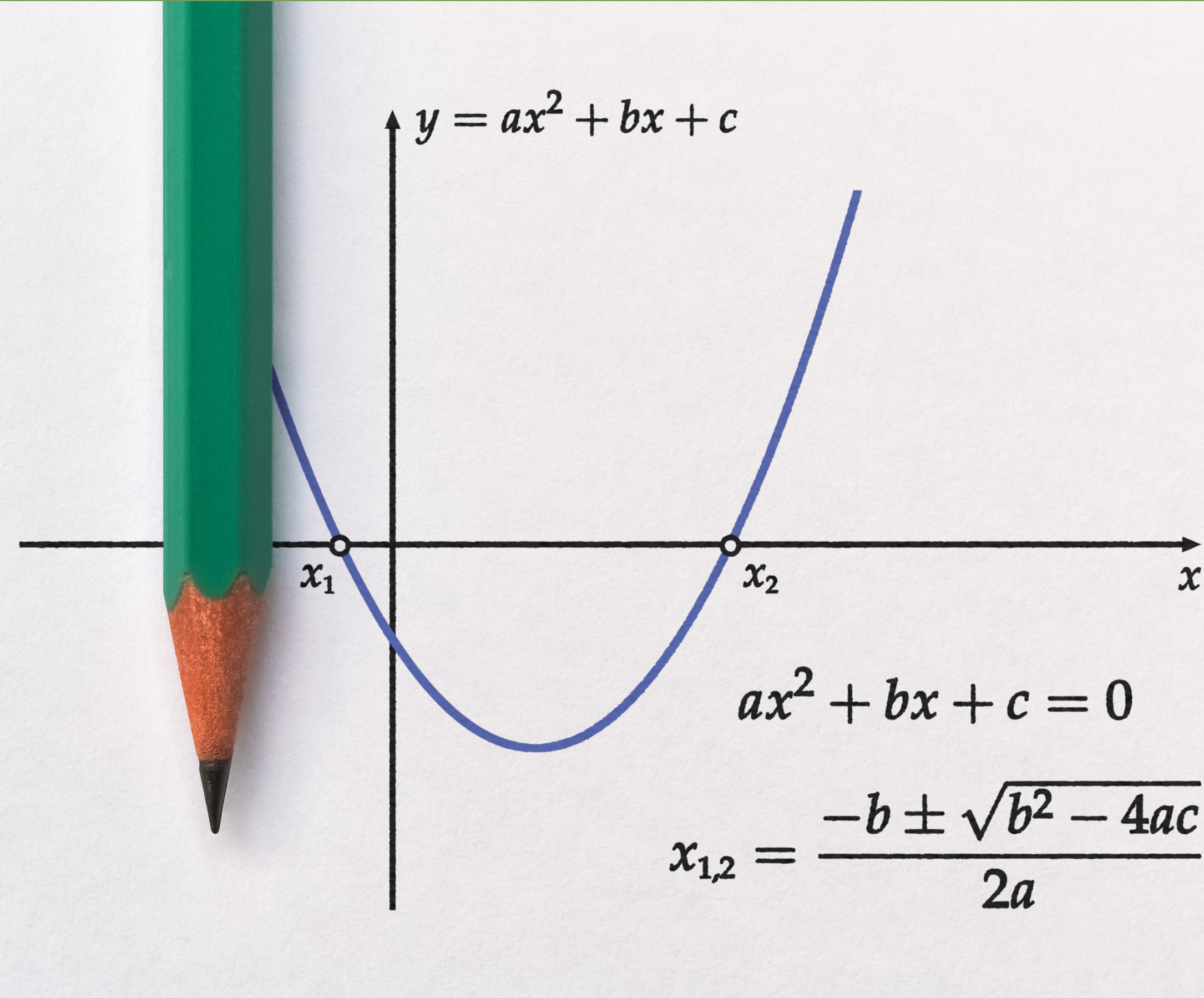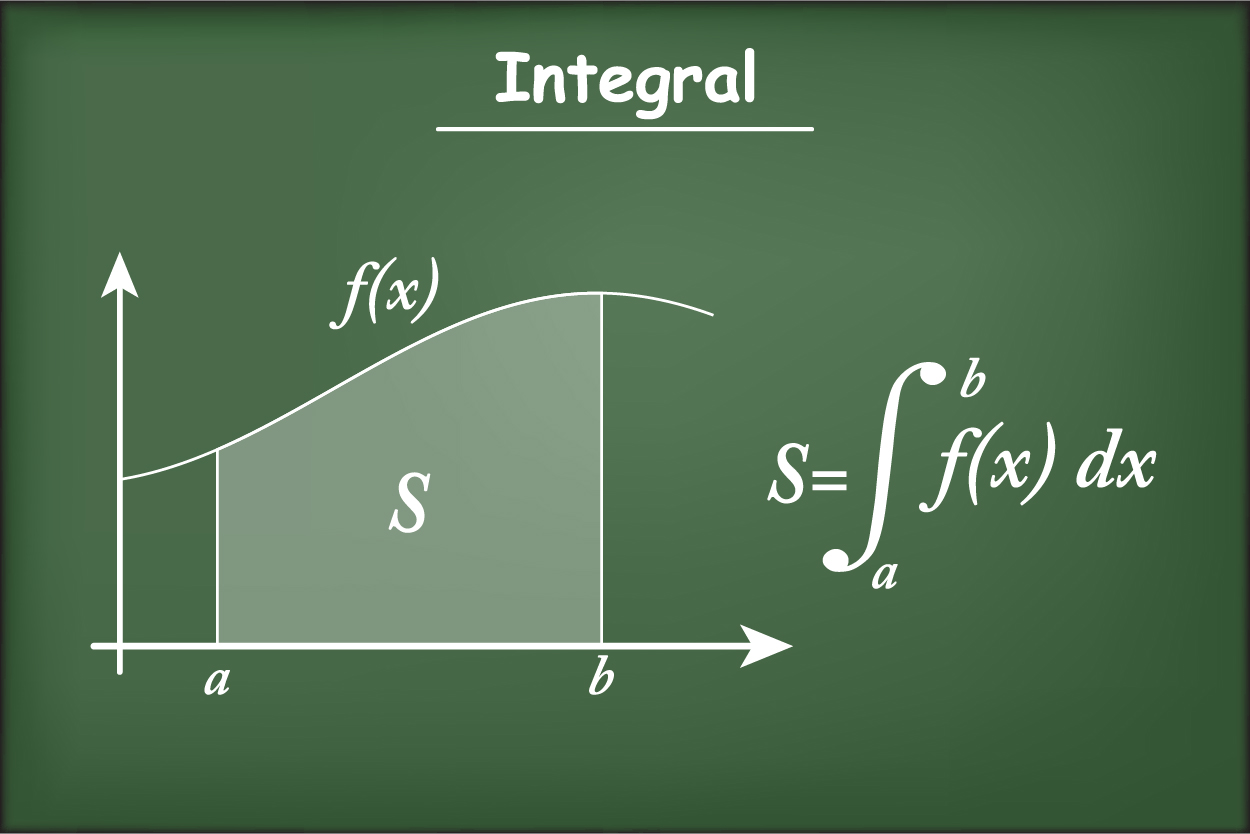
Python ile Sayısal İntegral
13 Şubat 2021
Geri Farklar ile Türev
20 Şubat 2021
İleri Farklar ile türev
Kabaca bahsedersek, ileri farklarda bir sonraki noktanın y kordinatından bulunulan noktanın y kordinatını çıkarıp, bunu x kordinatları farkına bölerek hesaplanıyor. Matematik olarak şöyle gösterilebilir.
f^{\prime}(x) \cong \frac{f\left(x_{i+1}\right)-f\left(x_{i}\right)}{x_{i+1}-x_{i}}=\frac{y_{i+1}-y_{i}}{x_{i+1}-x_{i}}
Şimdi yukarıdaki işlemi python için kodlayalım.
def forward(y, x):
dyf = np.zeros(len(x)-1)
for i in range(len(x)-1):
dyf[i] = (y[i + 1] - y[i]) / (x[i + 1] - x[i])
return dyf
Yukarıdaki fonksiyonu incelersek, fonksiyonun girdisi y ve x listesi olacak. Bu girdiler y ve x kordinatlarını içeren listeler. Fonksiyonun içerisinde ilk olarak türevleri hesaplandıkatan sonra depolamak için dyf adında bir boş array açıyoruz. Her noktanın türevini hesaplamak için bir sonraki noktayı kullanacağımız için, son noktada bir türev hesaplayamayacağız. Bu sebeple dyf’nin boyutu girdi olarak verilen listelerin boyutundan bir az olarak belirlendi.
Sonrasında for döngüsüyle yukarıda verilen denklemi aynen yazıyoruz ve döngüyü girdi olarak verilen listenin boyutundan bir eksik olarak belirliyoruz. Böylece her iterasyonda bir sonraki noktanın y değerinden bulunulan noktanın y değerini çıkartıp, aynı şekilde x değerlerini çıkartıp birbirine bölüyor ve bunu dyf’nin içinde depoluyor.
Ders 1.2: Geri Farklar Yöntemiyle Türev
Serdar Turgut İnce